Trees

     I think that the mathematics of fractal trees has probably been covered by about ten thousand people on the internet, but today, as I sat in the parking lot of the grocery store, with nothing but my notebook and pencil, I had access to the work of exactly   of them.  So I had a go.

     It's really not that hard, as it turns out. The number of points in a single level of an exponential tree is 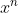, and from there, it's not enormously hard to figure out everything else about the tree. But here was my problem: how to create an algorithm to loop through all elements of an exponential tree. For that, I need to know how many points there are less than a certain index, defined by the parameters n, and i. n is the exponent, and i is the index of the point in that level. For instance, if it was on the 3rd level of a tree with the function 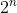, and an index of 3, it would be the third point on the level that contained 8 total points.

      After a little bit of messing around, but still before dad got back with the groceries, I realized that I could add up the values of all the levels before n, and add i - 1, and get the number of points less than i:

Again, simple stuff.

I don't have a simulation to show you today. =( Maybe tomorrow.