More on Numerical Integration

     So, in a previous post, I talked about the problem with translating differential equations into computer simulations. I did a lot of talking, but I didn't really say much that was useful. Here are four different methods of integrating the newtonian equations of motion, that are used frequently in simulation.

Explicit Euler

     Explicit Euler integration, according to Physics for Flash Games, Animation, and Simulations an explicit, first order accurate, and very fast integration scheme. Acceleration is calculated each frame in a simulation, but for our purposes, we can treat it as constant, and deal with a simple falling body, therefore

.

     Velocity can be simply integrated as:

     We if we split up each t into time steps, we then have:

     Going back to my textbook, that means that our position can be given as:

     This is Euler integration, and it is used by most programmers who don't need enormous accuracy or stability. And it's a good thing they don't, because if they did, they might need to try something new something like...

Position Verlet

     Position Verlet, usually just verlet, is a way of using not the first, but the second derivative of the acceleration equation to determine the motion of the particle. If we have our acceleration, and current position, we don't even need to look at the velocity, we have all the information we need to move the particle through the equations of motion. WRONG, we don't have all we need, inertia depends on velocity, and for velocity, we need to know where it was before. So, in verlet integration if:

,

     then, we skip the velocity:

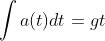      and work with the second derivative:

     Discretizing this turns out to be tricky, but my book has the answer, and, if you care, an implementation of Verlet Integration can be found here (https://sites.google.com/site/stylustechnology/recent-stuff/balls), where it is used to simulate a large pile of balls. Again, my book gives the result:

     Our final scheme is one that I have not yet implemented, but I get the idea.

Second Order Runge-Kutta Integration

     This is a way of taking a framework that looks a lot like euler integration, and making it more accurate. It takes the values of position and velocity at the beginning and end of a frame, and averages them. This is like taking the time step and halving it doubling the accuracy. It is also known as Improved Euler integration, and you will see that the final position and velocity equations are actually the Explicit Euler equations in disguise.

     First, define the values of position, velocity, and acceleration, at the beginning of the time step:

, 

,

     Then, recalculate all values at the end of the time step:

,

,

     Finally, use that to calculate velocity, then position:

,

.

     And there you have it, three numerical integration schemes, I hope I have managed to make this a little easier of a topic. There is also a fourth-order Runge-Kutta which is similar to the one that I have outlined, but that is a lot longer, and I don't feel like writing out all of the equations. Take a look for your self: http://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods#Common_fourth-order_Runge.E2.80.93Kutta_method. Or alternatively, write up an animation of your own, using one of these schemes, and when you have, comment with the link, and make sure to include your source code!

The Jacobs Ladder

     The Jacobs ladder is the toy where the top block, when rotated in the right direction, initiates a cascade that will travel all the way down the ladder to the bottom. I have had one kicking around our house for forever, I think I may have stolen it from one of my friends. I apologize to them, but they may forgive me when they realize the use to which I have put their toy.
     No, I have not made a jacobs ladder simulation, maybe some day, what I have done, with the help of another friend, is figured out exactly what's going on. We even made one, out of duck tape.
     So the basic jacobs ladder has six blocks. Each block has ribbons on it's sides. Unless it's a block at the end, then it only has ribbons on one side. This was what we knew going in, along with the guess that the ribbons must go through the center of the blocks in some sort of configuration.
     We wanted to be able to express this whole thing as a diagram, and then maybe a mathematical formulation, so that we could describe all of the possible states of a jacobs ladder, and all of the dynamics that turned one state into another.
     The first thing we discovered, however, is that there is only one possible state for the Jacob's Ladder, just one. You can rotate and reflect (flip) this state, but you still get the same situation of each block and each ribbon, just upside down and backwards.
     So we drew our diagram:

     This is a side-on view of the jacobs ladder, where you can see the splits in the blocks, the purple is the two-strand line, and the green is the one-strand line. With this diagram, it is easy to see that there is a sort of back loop thing, where either the purple or the green will loop back on itself. This is what gives the ladder is's miraculous cascade ability. We then created a mathematical representation, where each side that did not have a ribbon is called a 0, each side with one ribbon is a I, and each side with two ribbons is a II:

     From this diagram, you can easily see that in all non-0 blocks, the color on one side is the same as the color on the other. But what about during the cascade, when everything is weird? Well let's see...

     Just through observation, we can see that this situation breaks the rules of the numerical representation, but, luckily, the graphical representation gives us an easy way to draw this:

     So now we know everything we need to know, and all that is left for us to do is to actually make one. I might make a video about  this, we'll see...

   

Balls

     A giant pile of balls, neatly stacked into the hexagonal formation that all circles love to pack themselves into. This has been my goal for today. Not a big goal, but one that has successfully distracted me from working on something harder and more important, like the Marker And Cell simulation that I am probably going to finish (read: begin) around 2020.
     So. I have made rigid body ball simulations before, but they used Euler integration, and thus were not very stable. And, to simulate a giant pile of balls, you need stability. So, I had to find a better way. The way I found was Verlet Integration (could you have guessed).
     Verlet Integration, the process by which acceleration, position, and position  ago. This is, for some reason that I don't really understand, a really stable way of integrating the equations of motion.
     So that was the integration scheme I chose, and the rest of it turned out to be fairly simple: correct the balls positions to account for overlap, fix velocities to preserve impulses (a problem with Verlet as it turns out), and then do it again a few times to approach truly rigid bodies.
     So here's the actual demonstration. Warning, it could be stabler, drag around the balls and it might explode. It is also un-optimized, so I could have a lot bigger pile that I do right now, but, work in progress, here it is:
https://sites.google.com/site/stylustechnology/recent-stuff/balls

Shaving Time

So I'm working on a post right now about the Jacobs Ladder, because my friend and I have recently dissected the Jacobs Ladder mathematically. But in the mean time I would like to talk about numerical integration.
     What on earth is that? good question. If you know some calculus, you know that the integral has something to do with taking an infinite amount of slices of something and counting up their area. The process of integrating an equation will give you the end result, but not the whole motion. This motion is all of these infinite slices put together.
     Unfortunately, computers have a problem with infinity. So do I, so basically everything that you do in simulation can be described as coarse graining. Coarse graining is the process of taking something that's beautifully smooth, and making it all rough and regimented.
       Now one type of this that EVERY developer has to do, is temporal course graining. Also known as time stepping, this takes the current value of a temporally evolving function, say x(t), modifies it based on the rate of change (external forces, inertia) which we'll call x'(t) or v(t), then it waits awhile, then it does it again.
     Now we come back to integrals. Say we have the function:

 (1)

     Now, we, as the creator, can decree that there are no other forces in our world, therefore, integrating this is not that hard:

 (2)

     Seems easy right, add a power to the exponent, divide by that new exponent. But what if, after 3 seconds, at t = 3, the base function becomes:

  (3)

     Easy, right, now our integral is:

 (4)

     No problems there, we simply express all solutions to this equations as being (2), for all times less than 3, and (4), for all times greater than three. What's the big deal with that. Well, what if the base function changed after t = 6, and then changed again after t = 9, and kept changing, every time t equalled a multiple of nine?

     Perhaps you can see where I'm going with this, our equation is changing every three seconds, a three second time step.

     To understand the need for this, lets go back to the real world. In the real world, there are no time steps, time just keeps on going, you can't keep looking closer and closer until you find time's framerate, it just doesn't work, it's always smaller than you can look. Sort of like the dt in our equations, in fact, exactly like that. The dt shaves down the variable it's applied to, t in our case, and looks at it through all time. An infinite number of shavings, each with zero width.

     The laws of motion tell us that all objects in a state like to stay in that state, of either motion, or rest, unless another force acts on them. This is fine, but not useful for chaotic simulations, and most simulations used for computer graphics are, because in chaotic simulations there is a lot going on. Things almost never go in a straight line, and the equations determining (not governing: determining), the motion of these particles are always changing.

     Except they're not always changing, they are changing every time step, and teleporting from position to position, based on the computed rates of change for their velocities. The computer looks at things, changes them, waits, and then does it again, each time, it takes off a precisely allotted shaving, not infinitely small, actually rather large, and then does it again, then again, then again, then again.

     It's not that hard to see how this method would produce some errors, things might slip inside of other things, forces might be computed to be too big, or too small, distances might cancel and result in a divide by zero, all of these problems are solvable, but the problem of numerical integration is one that will never go away, because it would take an infinitely powerful computer to have infinitely small timesteps, and that doesn't seem on the horizon.

     This might seem a bit unfortunate for the programmer: he/she will never get a perfect simulation of something, but, for me, it is almost unbearably exciting, I am experimenting with a field of science and technology that will NEVER be done. There will always be room to advance, room to make new methods, new ideas to be tested, and there will always be a better way.

    That sounds like job security to me, thanks for reading. 

Fire

      I've spent my day trying to simulate fire. Fire is a hard thing to simulate. It goes every which way, it is hot, it is buoyant, it twirls and spins in free air. It is gone before you've seen it. Each one of these behaviors are things that the simulator has to find solutions to all these problems.
     First, there is the fact that everyone knows, namely, fire is hot, and heat rises. Heat rises because it is less dense than air, but the whole idea of Eulerian fluid simulation is to make things the density uniform at all points, that is, to make the fluid incompressible. So how do we account for temperature. I had no idea, so i cribbed the idea from someone else.
     The basic method turned out to be to take the density (that's density of smoke or fire, or fog, or whatever, floating around in the fluid), and treat it as the temperature. Once you know that, adding buoyancy is trivial, just introduce an upward force on every point proportional to the density at that point. This gives much better results than my earlier method, that of shooting the fire upwards, as if out of a garden... um flamethrower.
     The second problem is that, in most Eulerian, (read Jos Stammian) fluid simulation, the velocity field tends to be smooth, and vortexes tend to disappear almost immediately. This can be solved through grid-based vorticity confinement, which, I discovered is not actually that hard, and has to do with identifying and increasing curvature for all cells.
     The only remaining problem is that simple fluid simulations like to diffuse their density, but hate to loose track of it. No color disappears. I had to make it go away manually. A fairly simple coefficient-based decay function solved this problem, and voila, a little bit of fire on my screen.
     Here's the first stage of my solver, with, of course, the source code:
https://sites.google.com/site/stylustechnology/recent-stuff/eulerian-fluid-simulation

Hard

     Math is hard for some. Bach is hard for some. Quantum Mechanics is hard for everyone. Fluid simulation based on the discretization of the Navier-Stokes equations for fluid motion is very very hard.

     That is, they're hard for me, they might not be hard for others, in fact, I'm sure it isn't. Lots of people have came to understand the theory and practice of fluid simulation, and a lot of them have written papers on it. A lot of them have made videos of their simulations, and posted them on YouTube. But few, very  few that I have been able to find, have posted their source code, or specifics on exactly What. To. Do.

     Let me be clear, this is not a sentiment shared by all programmers, many masters of fluid simulation, including Mr. Grant Kot, as well as Brochu et al. who published their source code along with their paper. Other source code packages are there for the finding, but few are published in a place that is easy to locate.

     This blog is called X Squared Plus Why Squared, so Why does this happen. The answer seems fairly clear, and resolves into a sort of self-perpetuating cycle, which goes like this:

     A programmer decides to implement a fluid simulator, with little or no prior experience. The more experience with either simulation, programming, or mathematics, the easier it'll be, they work and work and work, research, and research and research, until they finally succeed. They then make a video about it, and post it on YouTube. In the comments section of the video, lots of people ask to see the source codes for this persons simulation, but he is now proud of his work, and does not oblige. He worked hard for what he eventually produced, and is now going to hold on to, and maybe monetize, his creation. This is perfectly understandable, but very unfortunate, because it keeps the magic and awesomeness of fluid simulation in just that realm: that of magic and awe.

     So, what's the answer? This is why I love Processing. Because it is impossible to publish a document with out including the source code. If everyone published a version of their fluid simulator in Processing, then this problem would simply go away, the cycle would break, and the internet would suddenly get very, very, very wet.

Trees

     I think that the mathematics of fractal trees has probably been covered by about ten thousand people on the internet, but today, as I sat in the parking lot of the grocery store, with nothing but my notebook and pencil, I had access to the work of exactly   of them.  So I had a go.

     It's really not that hard, as it turns out. The number of points in a single level of an exponential tree is , and from there, it's not enormously hard to figure out everything else about the tree. But here was my problem: how to create an algorithm to loop through all elements of an exponential tree. For that, I need to know how many points there are less than a certain index, defined by the parameters n, and i. n is the exponent, and i is the index of the point in that level. For instance, if it was on the 3rd level of a tree with the function , and an index of 3, it would be the third point on the level that contained 8 total points.

      After a little bit of messing around, but still before dad got back with the groceries, I realized that I could add up the values of all the levels before n, and add i - 1, and get the number of points less than i:

Again, simple stuff.

I don't have a simulation to show you today. =( Maybe tomorrow.

Perhaps

So.
     The regular person that I show new experimental equations to is not here, or contactable, I wanted to tell someone, so I decided, the world wide web would have to do.
     So, the problem is: how to find vortices (read whirlpools) in particle-based fluid simulations. There is a way to format vorticity confinement that involves tracking and introducing by means of a Eulerian grid. I don't like Eulerian grids, so I needed a way to do this without a background mesh.
     In smoothed particle hydrodynamics, values around a particle are found by means of kernel functions. I now need a kernel function that can characterize the vorticity around a particle AKA, how much the particles around is are spiraling around it. The real question is: How tangential are the velocities of each particles neighbors relative to that particle.
     It's the bell shaped curve. For particle velocities that are 90 degrees away from the direction that would point to the particle that we're looking at, the value would be at the top of the bell. But, for particle velocities that are either moving toward or away from the particle, the value would be low. You could also use this to measure divergence.
     So, here's my equation for vorticity:

          where sigma is adjustable near 1, and

     So, maybe that'll work, maybe it won't, we'll see.

Hunting for Answers

     Okay, so some of you have probably seen the movie Good Will Hunting. In that movie, he solves what is purported to be an incredibly difficult math problem. Actually, he solves two problems, but the one we are concerned with here is the second one. It isn't explained in the movie, but we can see that is must have something to do with lines and dots.
     All right, so what is the problem. Well, we'll sort out the wording, but it is:
          Draw all homeomorphically irreducible trees of size n = 10.
     Homeomorphically irreducible means that it does not have only two lines going to only one dot. A tree, for our purposes, is a map of lines and dots.
     So I gave it a try:

   And, it turns out not to be that hard. Try it yourself. Pick another number, other than ten. Try not to look up the answer on Google Images. Post your results.

Post results.

Oh, and here's a simulation of a blob: https://sites.google.com/site/stylustechnology/recent-stuff/blob

First post and some water

Hello, this is my blog
I'll put things on it.
Here's a fluid simulation:

https://sites.google.com/site/stylustechnology/recent-stuff/smoothed-particle-hydrodynamics