Hey, I Have A Blog!

I do, I really do, but I haven't really been putting that much on it. The reason was that I have been putting more work into some YouTube videos. Maybe you've heard of some of them, I made them with the help of these two kids, they are named Martin and Cora.

I am now working on two different video games. One is a short kind of online game, and the other, which is much in the planning stages, is a sandbox game that has to do with some stuff that's still totally secret, so I am not going to say any more on that matter.

The deadline for the sandbox game is whenever I finish it. So that's a bit of a bummer. But deal.

There are new things to play with on my website, and a new video game that I made for my friend Nick's birthday.

Here are the links: 

Martin and Cora: https://www.youtube.com/user/MartinAndCoraExplain

My website: www.stylustechnology.com

Nick's video game: https://sites.google.com/site/stylustechnology/home/secret

Have fun, 

      -Eli Davies

The Game of Life

     Hello, in the interest of trying everything that I can think of, I have created a platform for developing patterns using the Game of Life rules. This application is available here. Make sure to download the whole folder, and the load.txt file. You can load from text, load from simple images, and save and reload you're work, as well as pause and adjust the speed of animation. Enjoy

Just For Fun...

     So I put together this little demo, and this is a good one to take the trouble to download because it's fun. Or, at least, I think it's fun. It's based on the same engine as the pile-o-balls simulator, except this one uses springs. Every time you right click, the game generates an new shape for you to drag around, and every time you press the up or down arrow, the stiffness of the springs is raised or lowered.
     So take a look, it can't be that bad, right?
https://sites.google.com/site/stylustechnology/recent-stuff/spring-shapes

More on Numerical Integration

     So, in a previous post, I talked about the problem with translating differential equations into computer simulations. I did a lot of talking, but I didn't really say much that was useful. Here are four different methods of integrating the newtonian equations of motion, that are used frequently in simulation.

Explicit Euler

     Explicit Euler integration, according to Physics for Flash Games, Animation, and Simulations an explicit, first order accurate, and very fast integration scheme. Acceleration is calculated each frame in a simulation, but for our purposes, we can treat it as constant, and deal with a simple falling body, therefore

.

     Velocity can be simply integrated as:

     We if we split up each t into time steps, we then have:

     Going back to my textbook, that means that our position can be given as:

     This is Euler integration, and it is used by most programmers who don't need enormous accuracy or stability. And it's a good thing they don't, because if they did, they might need to try something new something like...

Position Verlet

     Position Verlet, usually just verlet, is a way of using not the first, but the second derivative of the acceleration equation to determine the motion of the particle. If we have our acceleration, and current position, we don't even need to look at the velocity, we have all the information we need to move the particle through the equations of motion. WRONG, we don't have all we need, inertia depends on velocity, and for velocity, we need to know where it was before. So, in verlet integration if:

,

     then, we skip the velocity:

      and work with the second derivative:

     Discretizing this turns out to be tricky, but my book has the answer, and, if you care, an implementation of Verlet Integration can be found here (https://sites.google.com/site/stylustechnology/recent-stuff/balls), where it is used to simulate a large pile of balls. Again, my book gives the result:

     Our final scheme is one that I have not yet implemented, but I get the idea.

Second Order Runge-Kutta Integration

     This is a way of taking a framework that looks a lot like euler integration, and making it more accurate. It takes the values of position and velocity at the beginning and end of a frame, and averages them. This is like taking the time step and halving it doubling the accuracy. It is also known as Improved Euler integration, and you will see that the final position and velocity equations are actually the Explicit Euler equations in disguise.

     First, define the values of position, velocity, and acceleration, at the beginning of the time step:

, 

,

     Then, recalculate all values at the end of the time step:

,

,

     Finally, use that to calculate velocity, then position:

,

.

     And there you have it, three numerical integration schemes, I hope I have managed to make this a little easier of a topic. There is also a fourth-order Runge-Kutta which is similar to the one that I have outlined, but that is a lot longer, and I don't feel like writing out all of the equations. Take a look for your self: http://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods#Common_fourth-order_Runge.E2.80.93Kutta_method. Or alternatively, write up an animation of your own, using one of these schemes, and when you have, comment with the link, and make sure to include your source code!

The Jacobs Ladder

     The Jacobs ladder is the toy where the top block, when rotated in the right direction, initiates a cascade that will travel all the way down the ladder to the bottom. I have had one kicking around our house for forever, I think I may have stolen it from one of my friends. I apologize to them, but they may forgive me when they realize the use to which I have put their toy.
     No, I have not made a jacobs ladder simulation, maybe some day, what I have done, with the help of another friend, is figured out exactly what's going on. We even made one, out of duck tape.
     So the basic jacobs ladder has six blocks. Each block has ribbons on it's sides. Unless it's a block at the end, then it only has ribbons on one side. This was what we knew going in, along with the guess that the ribbons must go through the center of the blocks in some sort of configuration.
     We wanted to be able to express this whole thing as a diagram, and then maybe a mathematical formulation, so that we could describe all of the possible states of a jacobs ladder, and all of the dynamics that turned one state into another.
     The first thing we discovered, however, is that there is only one possible state for the Jacob's Ladder, just one. You can rotate and reflect (flip) this state, but you still get the same situation of each block and each ribbon, just upside down and backwards.
     So we drew our diagram:

     This is a side-on view of the jacobs ladder, where you can see the splits in the blocks, the purple is the two-strand line, and the green is the one-strand line. With this diagram, it is easy to see that there is a sort of back loop thing, where either the purple or the green will loop back on itself. This is what gives the ladder is's miraculous cascade ability. We then created a mathematical representation, where each side that did not have a ribbon is called a 0, each side with one ribbon is a I, and each side with two ribbons is a II:

     From this diagram, you can easily see that in all non-0 blocks, the color on one side is the same as the color on the other. But what about during the cascade, when everything is weird? Well let's see...

     Just through observation, we can see that this situation breaks the rules of the numerical representation, but, luckily, the graphical representation gives us an easy way to draw this:

     So now we know everything we need to know, and all that is left for us to do is to actually make one. I might make a video about  this, we'll see...

   

Balls

     A giant pile of balls, neatly stacked into the hexagonal formation that all circles love to pack themselves into. This has been my goal for today. Not a big goal, but one that has successfully distracted me from working on something harder and more important, like the Marker And Cell simulation that I am probably going to finish (read: begin) around 2020.
     So. I have made rigid body ball simulations before, but they used Euler integration, and thus were not very stable. And, to simulate a giant pile of balls, you need stability. So, I had to find a better way. The way I found was Verlet Integration (could you have guessed).
     Verlet Integration, the process by which acceleration, position, and position  ago. This is, for some reason that I don't really understand, a really stable way of integrating the equations of motion.
     So that was the integration scheme I chose, and the rest of it turned out to be fairly simple: correct the balls positions to account for overlap, fix velocities to preserve impulses (a problem with Verlet as it turns out), and then do it again a few times to approach truly rigid bodies.
     So here's the actual demonstration. Warning, it could be stabler, drag around the balls and it might explode. It is also un-optimized, so I could have a lot bigger pile that I do right now, but, work in progress, here it is:
https://sites.google.com/site/stylustechnology/recent-stuff/balls

Shaving Time

So I'm working on a post right now about the Jacobs Ladder, because my friend and I have recently dissected the Jacobs Ladder mathematically. But in the mean time I would like to talk about numerical integration.
     What on earth is that? good question. If you know some calculus, you know that the integral has something to do with taking an infinite amount of slices of something and counting up their area. The process of integrating an equation will give you the end result, but not the whole motion. This motion is all of these infinite slices put together.
     Unfortunately, computers have a problem with infinity. So do I, so basically everything that you do in simulation can be described as coarse graining. Coarse graining is the process of taking something that's beautifully smooth, and making it all rough and regimented.
       Now one type of this that EVERY developer has to do, is temporal course graining. Also known as time stepping, this takes the current value of a temporally evolving function, say x(t), modifies it based on the rate of change (external forces, inertia) which we'll call x'(t) or v(t), then it waits awhile, then it does it again.
     Now we come back to integrals. Say we have the function:

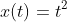
 (1)

     Now, we, as the creator, can decree that there are no other forces in our world, therefore, integrating this is not that hard:

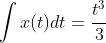
 (2)

     Seems easy right, add a power to the exponent, divide by that new exponent. But what if, after 3 seconds, at t = 3, the base function becomes:

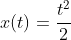
  (3)

     Easy, right, now our integral is:

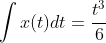
 (4)

     No problems there, we simply express all solutions to this equations as being (2), for all times less than 3, and (4), for all times greater than three. What's the big deal with that. Well, what if the base function changed after t = 6, and then changed again after t = 9, and kept changing, every time t equalled a multiple of nine?

     Perhaps you can see where I'm going with this, our equation is changing every three seconds, a three second time step.

     To understand the need for this, lets go back to the real world. In the real world, there are no time steps, time just keeps on going, you can't keep looking closer and closer until you find time's framerate, it just doesn't work, it's always smaller than you can look. Sort of like the dt in our equations, in fact, exactly like that. The dt shaves down the variable it's applied to, t in our case, and looks at it through all time. An infinite number of shavings, each with zero width.

     The laws of motion tell us that all objects in a state like to stay in that state, of either motion, or rest, unless another force acts on them. This is fine, but not useful for chaotic simulations, and most simulations used for computer graphics are, because in chaotic simulations there is a lot going on. Things almost never go in a straight line, and the equations determining (not governing: determining), the motion of these particles are always changing.

     Except they're not always changing, they are changing every time step, and teleporting from position to position, based on the computed rates of change for their velocities. The computer looks at things, changes them, waits, and then does it again, each time, it takes off a precisely allotted shaving, not infinitely small, actually rather large, and then does it again, then again, then again, then again.

     It's not that hard to see how this method would produce some errors, things might slip inside of other things, forces might be computed to be too big, or too small, distances might cancel and result in a divide by zero, all of these problems are solvable, but the problem of numerical integration is one that will never go away, because it would take an infinitely powerful computer to have infinitely small timesteps, and that doesn't seem on the horizon.

     This might seem a bit unfortunate for the programmer: he/she will never get a perfect simulation of something, but, for me, it is almost unbearably exciting, I am experimenting with a field of science and technology that will NEVER be done. There will always be room to advance, room to make new methods, new ideas to be tested, and there will always be a better way.

    That sounds like job security to me, thanks for reading.